"Soyons fiers d’être des Photoniciens !" par Jean-Claude FONTANELLA (promo 72)

Lors des derniers French Photonics Days à Strasbourg, les 17 et 18 octobre derniers, nous avons eu une très intéressante présentation de Bernard Kress, Directeur de l’Optical Engineering chez Google sur « Novel display architectures for small form factor smart glasses and AR headsets ». Vous pouvez retrouver cette présentation sur le site FPD 2023.

A cette occasion, Bernard Kress, qui est aussi l’actuel président du SPIE et fait donc la promotion de la photonique, a rappelé qu’il n’y avait pas de loi de Moore en photonique, mais qu’à bien des égards, la croissance des performances des dispositifs photoniques était aussi exponentielle, donnant lieu à un certain nombre de pseudo-lois moins connues

Bernard Kress aux French Photonics Days à Strasbourg (Crédit photo Fabrice Michel)

On peut discuter de la pertinence de ces « lois », souvent élaborées il y a plusieurs dizaines d’années, et de leur paternité. Elles deviennent difficiles à vérifier au fur et à mesure des changements de technologies et d’architecture (architectures 3D en micro-électroniques, fibres optiques multimodes…), mais elles donnent une vision synthétique des progrès fulgurants de la photonique, tout-à-fait équivalents à ceux de la microélectronique, et qui ont également transformé notre vie quotidienne (réseaux de communication à fibres optiques, éclairage par LED…).

Donc, soyons fiers de la contribution de la Photonique aux progrès de nos sociétés !

Petit résumé ci-dessous.

Rappel : la loi de Moore

Gordon Earle Moore,1929-2023, cofondateur d’Intel

Cette célèbre « loi », énoncée en 1975, prédit que le nombre de transistors sur une puce de Silicium double tous les deux ans. Même si l’on arrive aujourd’hui aux limites de la finesse de gravure, les architectures 3D permettent de poursuivre la densification des puces.

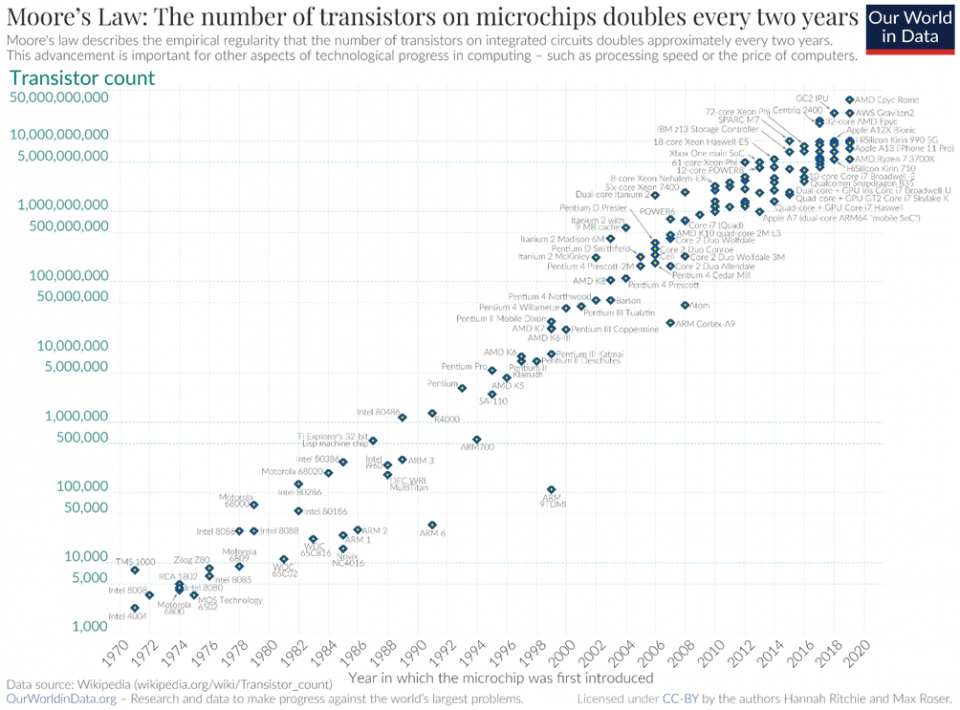
Source :  Max Roser, Hannah Ritchie — https://ourworldindata.org/uploads/2020/11/Transistor-Count-over-time.png, CC BY 4.0, https://commons.wikimedia.org/w/index.php?curid=98219918

La « loi de Keck »

Donald Keck, né en 1941, Directeur Technique de Corning

Cette « loi » stipule que le nombre de bits par seconde que peut transporter une fibre optique double tous les 1,5 ans. 

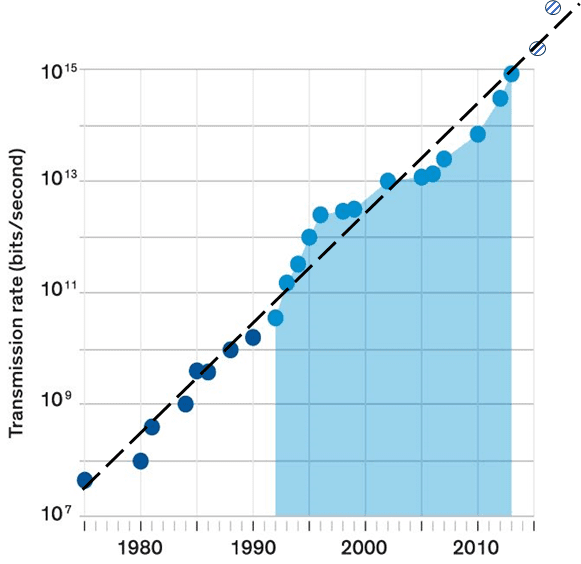
Graphique d’après : Is Keck’s Law Coming to an End ? - IEEE Spectrum 

La partie bleue correspond à l’introduction du multiplexage en longueur d’onde. La limite de Shannon étant atteinte depuis environ 2020, on est passé aux fibres multimodes / multicœurs et/ou aux câbles multifibres pour continuer de progresser rendant les comparaisons compliquées.

Les deux derniers points hachurés ont été rajoutés par moi-même (2,05 x 10^15 en 2015 (9.8km) et - 10,16 x 10^15 en 2017 (11km)) sur les conseils de Sébastien Bigo (promo 96) que je remercie pour ses commentaires. Le premier commentaire étant que ce graphique a été produit dès 1995 par Emmanuel Desurvire, inventeur des amplificateurs à fibres optiques dopées à l'erbium (EDFA), technologie clé des réseaux à fibre optique. Le second est que cette représentation est discutable : elle n’a de sens qu’à une distance donnée et la courbe ne dit rien à ce sujet. Le produit capacité x distance serait beaucoup plus pertinent (transmettre sur 6000 km ou 10 km, ce n’est pas du tout le même niveau de difficulté).

La « loi de Haitz »

Roland Haitz (1935-2015), d’origine allemande, a travaillé pour Texas Instrument, Hewlett Packard et Agilent Technologies

La quantité de lumière générée par un boîtier LED augmente d'un facteur 20 (voire 30) tous les 10 ans tandis que le coût par lumen décroit d'un facteur 10.

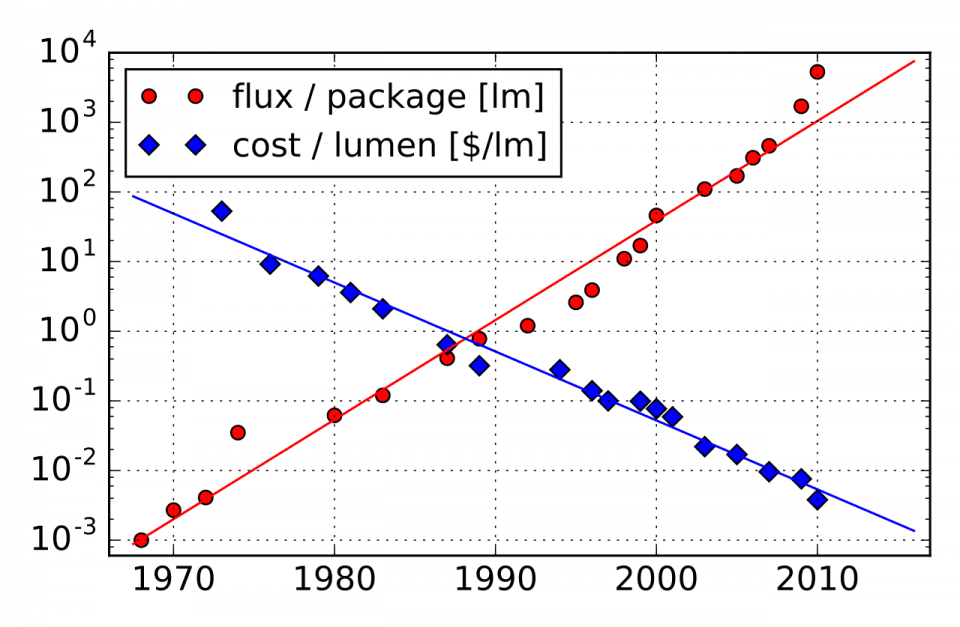
Source By Geek3 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=64876653

Ces courbes datent de 2010 et je n’ai pas trouvé de courbes plus récentes, ce qui indique probablement un plafonnement. A noter qu’en terme de rendement en lumen/W, les meilleures performances sont de l’ordre de 200 lm/W, proches du maximum théorique de 251 lm/W sur la bande 400-700nm =, voir  lumens-per-watt.pdf (ucsd.edu)

Une loi sans nom pour les grands télescopes

La surface de collection des télescopes astronomique double tous les 20 ans, ce qui fait un facteur un million en 400 ans entre la (deuxième) lunette de Galilée (diamètre 37mm) et l’Extremely Large Telescope de l’European Southern Observatory (39m).

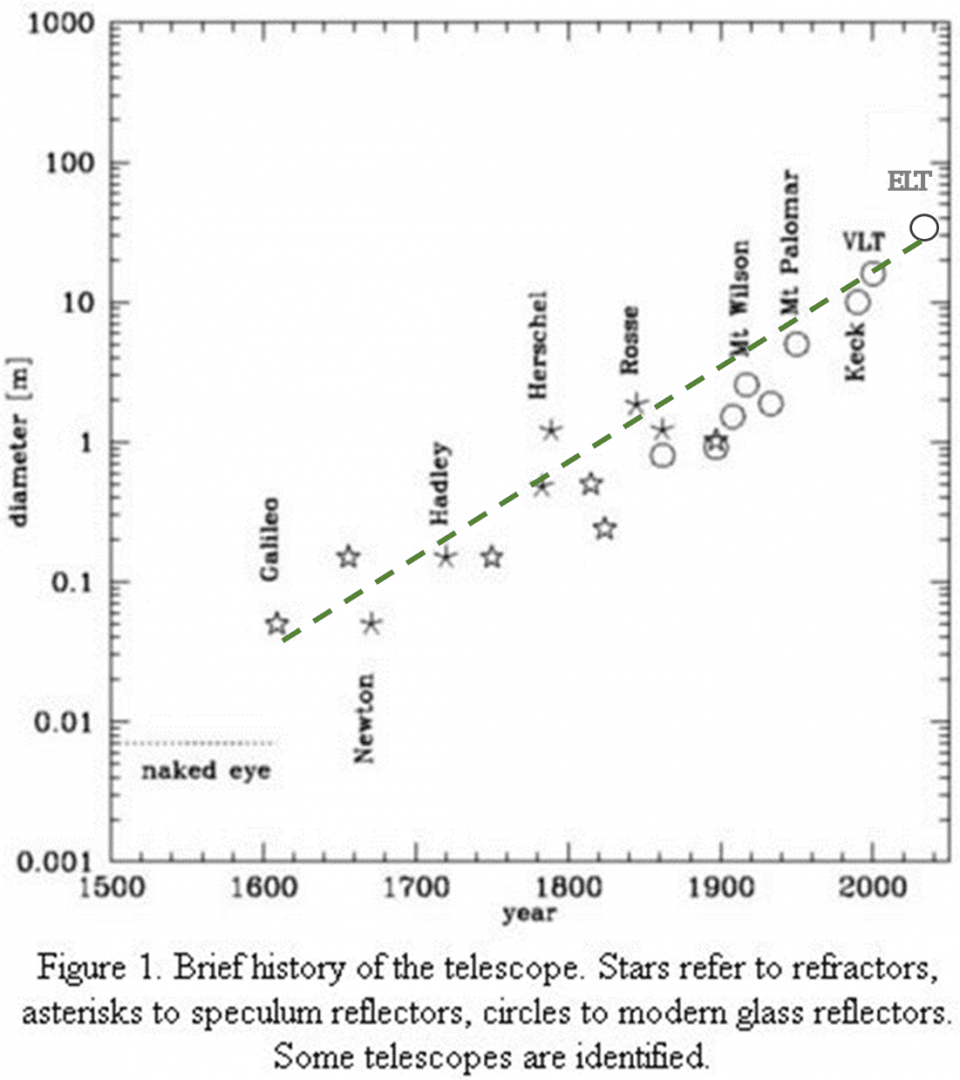
D’après document ESO (owl concept study (eso.org)

Ce doublement est aussi illustré sur la figure suivante qui regroupe les télescopes construits depuis plus de 100 ans

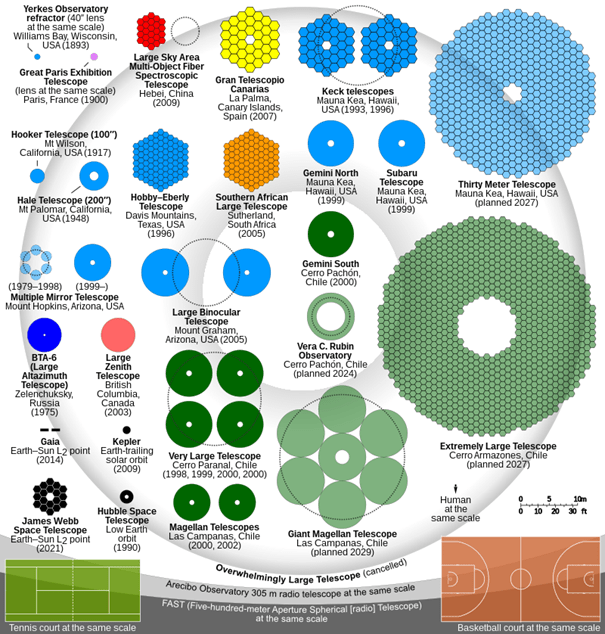Par Cmglee : data on holes in mirrors provided by an anonymous user from IP 71.41.210.146 — Travail personnel, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=33613161

Là aussi, on peut discuter de la pertinence de la comparaison, les technologies ayant évolué (lentille, miroir, miroir segmenté avec optique adaptative) et on ne prend pas en compte l’interférométrie optique qui permet d’atteindre des bases pouvant aller jusqu’à 200m.

A la différence des autres « lois » décrites précédemment, cette courbe décrit les performances d’une technologie qui n’est pas « tirée » par le marché civil.

Et on pourrait probablement d’autres « lois », par ex. sur la taille et le nombre de pixels des écrans, la résolution des spectromètres…

Article rédigé par Jean-Claude Fontanella (promo 72)